Solving Simultaneous Linear Equations
See also: matrix, Gauss-Jordan elimination, Geometric Linear Transformation
The calculator below will solve simultaneous linear equations with two, three and up to 10 variables if the system of equation has a unique solution.
For systems of equations with many solutions, please use the Gauss-Jordan Elimination method to solve it.
Please scroll down to read about various methods to solve simultaneous linear equations.
Simultaneous Linear Equation Solver
Choose the size of the system.
Please report any error to [email protected]
Methods to solve simultaneous linear equations
There are at least five methods to solve simultaneous linear equations.
For example, let's try to find the solution for the following set of simultaneous linear equations with 3 variables
Elimination method
As the name suggest, this method tries to eliminate variables until there's only 1 variable left.
First, look at the equations and try to find 2 equations which has the same coefficient (plus or minus) for the same variables. For example, see equations and . The coefficient for is and respectively. We can add the two equations to eliminate and we get equation .
Note that equation consists of variables and . Now we need another equation that has the same variables as equation . To get this we will eliminate from equation and . In equation and , the coefficients of are and respectively. In order to eliminate , we multiply equation by and then subtract equation from equation .
With equations and , we can now eliminate .
From equation we get . Now we can substitute this value of to equation to get the value for .
Finally, we can substitute the values of and to equation to get .
Hence the solution to the system of linear equations is , , .
Substitution method
First, let's re-arrange equation such that only 1 variable is on the left hand side.
Now let's substitute this to equation .
Similarly, substitute to equation .
Now let's re-arrange equation so that only 1 variable is on the left hand side.
Next, substitute this value of to equation .
Now that we have found , we can substitute this to equation to find .
Finally, we can substitute the value of and to equation to get the value of .
Graphical method
Solving a system of linear equation using graphical method is done by drawing the lines or planes that represent each equation. The solution is the coordinates of the intersection of the lines or planes.
For simplicity sake, let's consider a system of linear equations with two variables.
Plot the lines of these two equations.
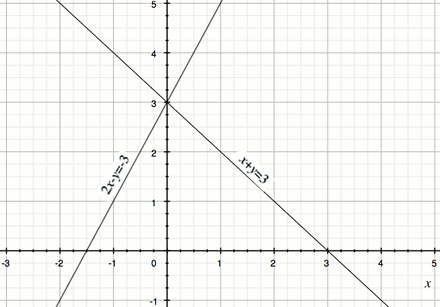
As shown on the graph, the two lines intersect at point . This is the solution to the system of linear equations, i.e. , .
For system of linear equations with three variables, the solution is the point of intersection of the three planes that represent each equation.
Inverse Matrix Method
The system of linear equations defined by equations , and can be expressed in matrix form as follows.
The solutions set is the matrix . To isolate alone on one side of the equation, we multiply both sides of the equation with the inverse of matrix .
Now to find we need to find . Please check the matrix page to learn how to find the inverse of a matrix.
Hence the solution set is , , .
Gaussian Elimination / Gauss-Jordan Elimination
The system of linear equations defined by equations , and can be expressed in augmented matrix form as follows.
By performing a series of row operations (Gaussian elimination), we can reduce the above matrix to its row echelon form.
We can then do back substitution to get the value of all the unknowns / variables or we can perform further row operations until the matrix is in reduced row echelon form (using Gauss-Jordan Elimination).
By doing the Gauss-Jordan elimination, we get the solution of the system of equations on the last column: , , .
To see step by step row operations involved, please see the Gauss-Jordan Elimination page.
Confused and have questions? We’ve got answers. With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field.
See also: matrix, Gauss-Jordan elimination, Geometric Linear Transformation
