參見：矩陣、高斯－若爾當消元法、幾何線性映射

---

你可使用下面的求解器對二元一次方程組、三元一次方程組⋯⋯十元一次方程組進行求值：

請見如下線性方程祖求解方法。

---

線性方程祖求解方法

求解線性方程祖至少有下面的五種方法：

• 消元法
• 代入法
• 圖象法
• 逆矩陣法
• 高斯消元法／高斯－若爾當消元法

例如，現在我們來對下面這個三元一次方程組進行求解：

$$\{\begin{array}{rrrrrll}x& +& y& -& z& =1& \text{(1)}\\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}\\ -4<!--\; InvisibleTimes\; -->x& -& y+& 3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\end{array}$$

---

消元法

顧名思義，這種方法就是盡量消去方程組中的未知數，使未知數的個數減少到一個。

首先，觀察這個方程組，找出其中某一未知數係數的值相等的兩個方程式。我們來看看等式$\text{(1)}$和$\text{(3)}$，這兩個方程式中 $y$ 的係數分別為$1$和$-1$，把两个式子相加就得到等式$\text{(4)}$。

$$\begin{gathered} \begin{array}{rrrrrll}x& +& y& -& z& =1& \text{(1)}\\ -4<!--\; InvisibleTimes\; -->x& -& y& +& 3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\end{array} \\ \text{------------------------}+ \\ \begin{array}{rrrrrll}-3<!--\; InvisibleTimes\; -->x& \phantom{+}& \phantom{0}& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}\end{array} \end{gathered}$$

請注意，現在$\text{(4)}$只有 $x$和$z$兩個未知數，只需要再找一個含有同樣未知數的方程式即可。因此我們嘗試就把$\text{(1)}$和$\text{(2)}$的 $y$消掉。以上兩個式子$y$的係數分別為$1$和$3$，為了消掉$y$，我们把$\text{(1)}$乘以$3$。

$$\begin{array}{rrrrrlll}x& +& y& -& z& =1& \text{(1)}& \text{× 3}\\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}& \end{array}$$
$$\begin{gathered} \begin{array}{rrrrrlll}3<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 3<!--\; InvisibleTimes\; -->z& =3& \text{(1)}& \\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}& \end{array} \\ \text{------------------------}- \\ \begin{array}{rrrrrlll}-5<!--\; InvisibleTimes\; -->x& \phantom{+}& \phantom{0<!--\; InvisibleTimes\; -->y}& +& 3<!--\; InvisibleTimes\; -->z& =2& \text{(5)}& \end{array} \end{gathered}$$

通過$\text{(4)}$和$\text{(5)}$可以消掉$z$：

$$\begin{array}{rrrrrl}-3<!--\; InvisibleTimes\; -->x& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}& \text{× 3}\\ -5<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->z& =2& \text{(5)}& \text{× 2}\end{array}$$
$$\begin{gathered} \begin{array}{rrrrrl}-9<!--\; InvisibleTimes\; -->x& +& 6<!--\; InvisibleTimes\; -->z& =6& \text{(4)}& \\ -10<!--\; InvisibleTimes\; -->x& +& 6<!--\; InvisibleTimes\; -->z& =4& \text{(5)}& \end{array} \\ \text{------------------------}- \\ \begin{array}{rrrrrl}\phantom{+01<!--\; InvisibleTimes\; -->}x& \phantom{+}& \phantom{0<!--\; InvisibleTimes\; -->z}& =2& \text{(6)}& \end{array} \end{gathered}$$

得到$x=2$後將它代入$\text{(4)}$中，求出$z$的值:

$$\begin{array}{rrrll}-3<!--\; InvisibleTimes\; -->\left(2\right)& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}\\ -6& +& 2<!--\; InvisibleTimes\; -->z& =2& \\ & & 2<!--\; InvisibleTimes\; -->z& =2+6& \\ & & 2<!--\; InvisibleTimes\; -->z& =8& \\ & & z& =8÷2& \\ & & z& =4& \end{array}$$

最後將$z$的值代入$\text{(1)}$求出$y$：

$$\begin{array}{rll}2+y-4& =1& \text{(1)}\\ y& =1-2+4& \\ y& =3& \end{array}$$

因此，該方程組的解是$x=2$，$y=3$，$z=4$。

---

代入法

首先，將方程式$\text{(1)}$進行移項變形，使得方程式的左邊只有一個未知數。

$$\begin{array}{rl}x=1-y+z& \text{(1)}\end{array}$$

現在將它代入$\text{(2)}$中。

$$\begin{array}{rll}8<!--\; InvisibleTimes\; -->\left(1-y+z\right)+3<!--\; InvisibleTimes\; -->y-6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}\\ 8-8<!--\; InvisibleTimes\; -->y+8<!--\; InvisibleTimes\; -->z+3<!--\; InvisibleTimes\; -->y-6<!--\; InvisibleTimes\; -->z& =1& \\ -5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->z& =1-8& \\ -5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->z& =-7& \text{(4)}\end{array}$$

同樣地，把$x$代入$\text{(3)}$。

$$\begin{array}{rll}-4<!--\; InvisibleTimes\; -->\left(1-y+z\right)-y+3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\\ -4+4<!--\; InvisibleTimes\; -->y-4<!--\; InvisibleTimes\; -->z-y+3<!--\; InvisibleTimes\; -->z& =1& \\ 3<!--\; InvisibleTimes\; -->y-z& =1+4& \\ 3<!--\; InvisibleTimes\; -->y-z& =5& \text{(5)}\end{array}$$

再將$\text{(5)}$變形，使得方程式左邊只有一個未知數

$$\begin{array}{rl}z=3<!--\; InvisibleTimes\; -->y-5& \text{(5)}\end{array}$$

接下來，我們將以上$z$的代數式代入$\text{(4)}$。

$$\begin{array}{rll}-5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->\left(3<!--\; InvisibleTimes\; -->y-5\right)& =-7& \text{(4)}\\ -5<!--\; InvisibleTimes\; -->y+6<!--\; InvisibleTimes\; -->y-\mathrm{10}& =-7& \\ y& =-7+10& \\ y& =3& \end{array}$$

既然已經求出$y$值，我們可以將它代入$\text{(5)}$解出$z$。

$$\begin{array}{rll}z& =3<!--\; InvisibleTimes\; -->\left(3\right)-5& \text{(5)}\\ z& =9-5& \\ z& =4& \end{array}$$

最後，我們將$y$和$z$的值代入$\text{(1)}$求出$x$。

$$\begin{array}{rll}x& =1-3+4& \text{(1)}\\ x& =2& \end{array}$$

因此，方程組的解為：$x=2$，$y=3$，$z=4$。

---

圖象法

圖象法就是把各方程式用圖象或平面圖表示出來，其交點也就是方程式的解。

先以下面這個簡單的二元一次方程組為例

$$\{\begin{array}{rrrr}x& +& y& =3\\ 2<!--\; InvisibleTimes\; -->x& -& y& =-3\end{array}$$

畫出這兩個方程式的圖象。

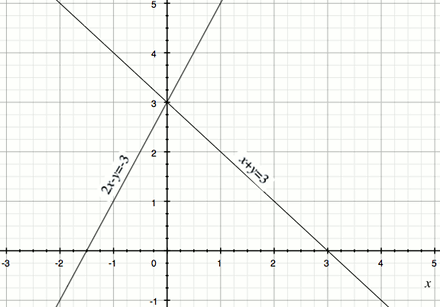
如圖所示，兩條直線的交點坐標是$(0,3)$，即該線性方程組的解為$x=0$，$y=3$。

對於三元一次線性方程組，它的解也就是代表各方程式的三個平面的交點。

---

逆矩陣法

運用矩陣公式$AB=C$可將線性方程組$\text{(1)}$，$\text{(2)}$，$\text{(3)}$可以表示成如下形式。

$$\begin{array}{rl}AB& =C\\ \left(\begin{array}{rrr}1& 2& -1\\ 8& 3& -6\\ -4& -1& 3\end{array}\right)<!--\; InvisibleTimes\; -->\left(\begin{array}{c}x\\ y\\ z\end{array}\right)& =\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\end{array}$$

方程組的解就是矩陣$B$。 為了使$B$單獨出現在等式的一邊，我們將等式兩邊同時乘以矩陣$A$ 的逆矩陣。

$$\begin{array}{rl}{A}^{-1}AB& =A^{-1}C\\ B& =A^{-1}C\end{array}$$

在求$B$之前我們需要先找到$A^{-1}$。（參見矩陣查看如何找出逆矩陣）

$$\begin{array}{rl}{A}^{-1}& =\left(\begin{array}{rrr}-3& 2& 3\\ 0& 1& 2\\ -4& 3& 5\end{array}\right)\\ B& =\left(\begin{array}{rrr}-3& 2& 3\\ 0& 1& 2\\ -4& 3& 5\end{array}\right)<!--\; InvisibleTimes\; -->\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\\ B& =\left(\begin{array}{c}2\\ 3\\ 4\end{array}\right)\end{array}$$

因此，方程組的解為： $x=2$， $y=3$， $z=4$。

此種方法適用于$n$元線性方程組的求解。以上所提供的求解器就是使用逆矩陣法進行求解。

---

高斯消元法／高斯－若爾當消元法

運用增廣矩陣公式$A$可將線性方程組$\text{(1)}$，$\text{(2)}$，$\text{(3)}$可以表示成如下形式。

$$A=\left(\begin{array}{rrrrr}1& 1& -1& \text{|}& 1\\ 8& 3& -6& \text{|}& 1\\ -4& -1& 3& \text{|}& 1\end{array}\right)$$

通過進行一系列的行變換（高斯消元法），我們可以將以上矩陣簡化成它的階梯形矩陣。

$$A=\left(\begin{array}{rccll}1& 0.375& -0.75& \text{|}& 0.125\\ 0& 1& -0.4& \text{|}& 1.4\\ 0& 0& 1& \text{|}& 4\end{array}\right)$$

接下來我們可以代入求出所有未知數的值，或者也可以繼續使用高斯－若爾當消元法進行行變換，直到該矩陣成為行簡階梯性形式。

$$A=\left(\begin{array}{rrrrr}1& 0& 0& \text{|}& 2\\ 0& 1& 0& \text{|}& 3\\ 0& 0& 1& \text{|}& 4\end{array}\right)$$

通過運用高斯－若爾當消元法，我們從最後一行中得到該方程組的解為$x=2$， $y=3$， $z=4$。

請參見高斯－若爾當消元法查看該題列變換的詳細步驟。

Jimmy Sie（著）
Amanda Huang（譯）

參見：矩陣、高斯－若爾當消元法、幾何線性映射